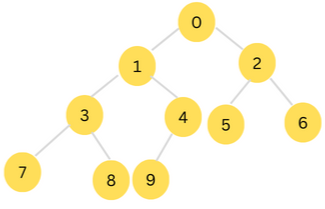
Tree data structure

DS & Algorithms

Algorithm Analysis

Overview

Complexity Functions

Big Oh Notation

Stacks & Queues

Stack

Fixed-length Stack

Queue

Deque

Linked Lists

singly-linked list

Doubly-Linked list

Circularly linked list

Linked List vs Array

Trees

Introduction

treelib

traversal algorithms

Binary Trees

Inorder traversal

Binary Search Trees

Sorting&Searching

Introduction

bubble sort

selection sort

insertion sort

merge-sort

tree data structure

The tree is one of the most important non-linear data structures. It is commonly used to represent hierarchical data.

Trees begins with a root node at the top and child nodes branching off below. This is analogous to a family tree, where the root node represents a common ancestor, and the child nodes represent descendants. Actually, family terminologies are pretty common in the tree data structure.

Abraham
├─ Ishmael
│  ├─ Nebaioth
│  ├─ Kedar
│  └─ Mishma
├─ Isaac
│  ├─ Jacob
│  │  ├─ Reuben
│  │  ├─ Joseph
│  │  └─ Judah
│  └─ Esau
│     ├─ Eliphaz
│     ├─ Jaalam
│     └─ Korah
└─ Zimran

The above section shows a non-complete family tree of Abraham's descendants.

Tree definitions and features

Tree data structure represents hierarchical data.

The elements in a tree are referred to as nodes.

Trees are identified by the following properties.

Each tree has a root node.
Each node apart from the root node has a parent node.
Each node is a parent of zero or more children nodes.

Each node contains the actual value and additional fields to reference its children nodes.

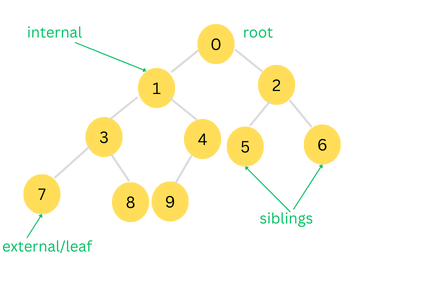
Node Terminologies and Relationships

Two nodes that are children of the same parent are called siblings.

If a node has no children it is referred to as external or leaf node. If a node has one or more children it is referred to as an internal node.

Tree relationships

Recursion is very important and widely used in various tree algorithms and operations.

Node a is an ancestor of node b, if a is an ancestor of b's parent. Conversely, node b is a descendant of node a if a is an ancestor of b. This relationship is usually determined using recursion.

A link between two nodes is known as edge.

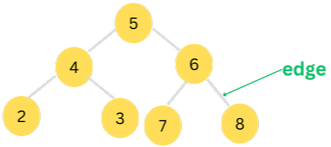
edge in tree terminologies

The height of a particular node is the number of edges on the longest path from that node to a leaf node.

The depth of a node is the number of edges from the root to that node.

The tree Abstract Data Type

An abstract data type is a higher level description of a data structure without including implementation details. In this section we will look at the various operations that are relevant to a tree data structure.

Basically, an implementation of a tree should support the following operations/methods.

T.root() - Returns a reference to the root node of the tree.
T.is_root(n) - Return True if node n is the root, else False.
T.parent(n) - Return a reference to the parent of node n.
T.children(n) - Return an iterator that yields the children of node n.
T.is_leaf(n) - Return True if n is a leaf node, else False.
T.num_children(n) - Return the number of children of node n.
T.is_empty() - return True if the tree is empty, else False.
len(T) - Return the number of all elements in the tree.
iter(T) - Return an iterator that yields all the elements in the tree.

Types of trees

In the above sections, the tree data structure is described in a general way. But for most practical purposes , trees are usually implemented in a specialized ways optimized based on the properties of the represented data set.

The following section highlights some common types of trees.

Binary trees

Binary trees are the most common manifestation of the tree data structure.

In a binary tree, each node, has at most two children: a left child and a right child.

the following is an example of a binary tree.

Binary trees are very efficient for search and sort operations, as they have a logarithmic time complexity for these operations. Binary trees can be easily balanced to ensure optimal performance.
Binary Search Trees

A binary search tree is a special type of binary tree that is optimized for searching. In this type of tree, the values of the left subtree are always smaller than the value of the parent node, while the values of the right subtree are always larger.

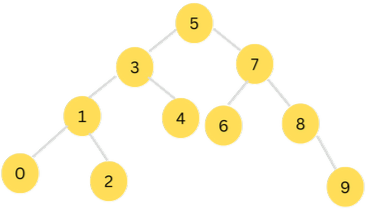
If you observe the above diagram you will see that at any point, the left subtree contains values that are smaller than parent's value, and the right subtree values are larger.

This pattern, makes it easier to determine which direction to traverse the tree in order to find a specific value. The property makes binary search trees far more efficient for search operations compared to other types of binary trees as well as other data structures.
Heaps

A heap is a specialized tree data structure that is very useful for implementing priority queues. There are two type of heaps, min-heap and max-heap.

In a min-heap, the value of the parent node is always smaller than or equal to the value of its child nodes. This means that the root node of a min-heap will always have the smallest value.

The above example shows a min-heap.

In a max-heap, the value of the parent node is always greater than or equal to the value of its child nodes. Thus, the root node will always have the largest value in the heap.

The ordering rule of a heap tree allows for efficient insertion and deletion operations, as well as finding the minimum or maximum value in the heap in constant time.

It is commonly used for efficient implementation of priority queues.
Splay trees

A splay tree is a self-adjusting type of binary search tree that automatically rearranges its structure based on recently accessed nodes. This allows for faster access to frequently used nodes.

In the following articles we will implement various type of trees in Python.