A Tree is a non-linear data structure that is normally used to represent hierarchical data.
In non-linear data structures, elements do not have a simple next-previous relationship like in arrays or linked lists. Thus to traverse through the elements in a tree, we need to use specialized algorithms.
Consider if we have a tree structure like one shown below:
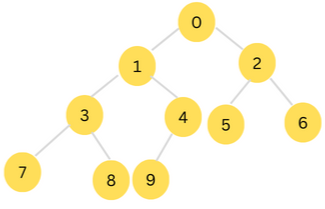
Tree traversal refers to the process of visiting every node in a tree exactly once. There are various important types of tree traversal algorithms, they includes:
- Breadth-First Traversal
- Pre-Order Traversal
- Post-Order Traversal
Before we look at the traversal algorithms we will first need to be able to implement trees.
In this article we will use the treelib package to represent trees and nodes. This package does not exist in the standard library, it can be installed using the following pip command.
pip install treelibcreating a tree
#import the Tree class
from treelib import Tree
#create a tree object
T = Tree()
#add nodes.
T.create_node(data = 0, identifier = '0')
T.create_node(data =1, identifier = '1', parent = '0')
T.create_node(data = 2, identifier = '2', parent = '0')
T.create_node(data = 3, identifier = '3', parent = '1')
T.create_node(data = 4, identifier = '4', parent = '1')
T.create_node(data = 5, identifier = '5', parent = '2')
T.create_node(data = 6, identifier = '6', parent = '2')
T.create_node(data = 7, identifier = '7', parent = '3')
T.create_node(data = 8, identifier = '8', parent = '3')
T.create_node(data = 9, identifier = '9', parent = '4')
#display the tree
print(T)The create_node() method of tree creates a new node and links it to the relevant existing nodes. It has the following syntax:
T.create_node(tag = None, identifier = None, parent = None, data = None)tag |
A human readable representation of the node. It defaults to None. |
identifier |
A unique identifier of a node in the tree. If not given, a unique random identifier is auto-generated. |
parent |
The identifier of this node's parent node. |
data |
The value stored by the node. |
In addition to the create_node() method, we will also use the following method of treelib.Tree objects when implementing the traversal algorithms.
T.get_node(identifier) |
Returns the node whose identifier is given as argument. Raises an exception if no such node exists. |
T.children(identifier) |
Returns a list containing all children of the node whose identifier is given as argument. |
Breadth-first Traversal
Breadth-First traversal is also referred to as Level-Order traversal. This is the easiest traversal mode to understand but it is slightly hard to implement compared to the rest.
In breadth-first traversal, the nodes are visited Level-by-Level, starting from the root node. At each level, the nodes are visited starting from the leftmost node going to the rightmost node.
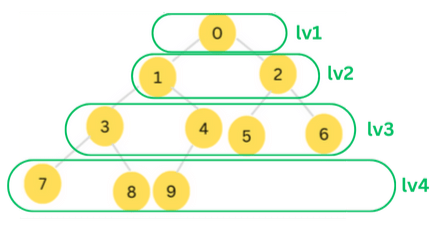
With breadth-first traversal, the nodes in the above tree would be visited in the following sequence:
0,1, 2, 3, 4, 5, 6, 7, 8, 9
Implement breadth-first traversal
The breadth-first traversal algorithm can be implemented by following the steps outlined below:
- Create an empty queue.
- Enqueue the root node into the queue.
- While the queue is not empty, do the following steps:
- Dequeue a node from the queue.
- process the node. e.g display it.
- Get all the children nodes of the dequeued node.
- For each child node, enqueue it into the queue.
- Once the queue is empty, the traversal is complete.
Enqueue and dequeue operations are used to add and remove an element from a queue, respectively. Enqueue operation adds an element at the back of the queue while dequeue operation removes the element at the front of the queue.
The dequeue (pronounced "dee-kew") operation should not be confused with deque(pronounced as "deck") which is a data structure that represent a double-ended queue.
In our implementation of breadth_first(), we will use collections.deque object as a queue. We will enqueue an element by adding it at the back of the deque using deque.append() method, the deque.popleft() will be used to perform a dequeue operation.
Implement breadth_first()
#import the deque class
from collections import deque
def breadth_first(T):
#create an empty queue
Q = deque()
Q.append(T.get_node(T.root)) #enqueue root node
while len(Q) > 0:
current = Q.popleft() #dequeue the front node
print(current.data)
for child in T.children(current.identifier):
Q.append(child) Using breadth_first()
#import the Tree class
from treelib import Tree
from collections import deque
#create a tree object
T = Tree()
#add nodes.
T.create_node(data = 0, identifier = '0')
T.create_node(data =1, identifier = '1', parent = '0')
T.create_node(data = 2, identifier = '2', parent = '0')
T.create_node(data = 3, identifier = '3', parent = '1')
T.create_node(data = 4, identifier = '4', parent = '1')
T.create_node(data = 5, identifier = '5', parent = '2')
T.create_node(data = 6, identifier = '6', parent = '2')
T.create_node(data = 7, identifier = '7', parent = '3')
T.create_node(data = 8, identifier = '8', parent = '3')
T.create_node(data = 9, identifier = '9', parent = '4')
breadth_first(T) #Implementation of breadth_first() function is omitted, refer to the previous section0
├── 1
│ ├── 3
│ │ ├── 7
│ │ └── 8
│ └── 4
│ └── 9
└── 2
├── 5
└── 6
Breadth-first:
0
1
2
3
4
5
6
7
8
9
Pre-order Traversal
In Pre-order traversal, we start by visiting the root node, then recursively traverse the subtrees rooted at the children of the root.
Consider our example tree shown below:

With pre-order traversal for the entire tree, the nodes will be visited in the following order.
0, 1, 3, 7, 8, 4, 9, 2, 5, 6
One important aspect of the pre-order traversal is that it can be performed for a subtree instead of the entire tree. For example, the pre-order traversal of node "1" above, will yield:
1, 3, 7, 8, 4, 9
The pre-order algorithm can be implemented recursively through the following steps:
- Visit the root node.
- Recursively visit all sub-trees rooted on the children of the root.
def pre_order(T, nid):
print(T.get_node(nid).data)
for child in T.children(nid):
pre_order(T, child.identifier)
#nid refers to "node identifier"In the above example, the pre_order() method takes in two arguments, the tree and nid, which is the identifier of the node whose subtree is to be traversed in pre-order.
pre_order() for entire tree
#import the Tree class
from treelib import Tree
#create a tree object
T = Tree()
#add nodes.
T.create_node(data = 0, identifier = '0')
T.create_node(data =1, identifier = '1', parent = '0')
T.create_node(data = 2, identifier = '2', parent = '0')
T.create_node(data = 3, identifier = '3', parent = '1')
T.create_node(data = 4, identifier = '4', parent = '1')
T.create_node(data = 5, identifier = '5', parent = '2')
T.create_node(data = 6, identifier = '6', parent = '2')
T.create_node(data = 7, identifier = '7', parent = '3')
T.create_node(data = 8, identifier = '8', parent = '3')
T.create_node(data = 9, identifier = '9', parent = '4')
print(T)
print("Pre-order:")
pre_order(T, T.root) #Implementation of pre_order() function is omitted, refer to the previous section0
├── 1
│ ├── 3
│ │ ├── 7
│ │ └── 8
│ └── 4
│ └── 9
└── 2
├── 5
└── 6
Pre-order:
0
1
3
7
8
4
9
2
5
6
pre-order() for a subtree
#import the Tree class
from treelib import Tree
#create a tree object
T = Tree()
#add nodes.
T.create_node(data = 0, identifier = '0')
T.create_node(data =1, identifier = '1', parent = '0')
T.create_node(data = 2, identifier = '2', parent = '0')
T.create_node(data = 3, identifier = '3', parent = '1')
T.create_node(data = 4, identifier = '4', parent = '1')
T.create_node(data = 5, identifier = '5', parent = '2')
T.create_node(data = 6, identifier = '6', parent = '2')
T.create_node(data = 7, identifier = '7', parent = '3')
T.create_node(data = 8, identifier = '8', parent = '3')
T.create_node(data = 9, identifier = '9', parent = '4')
print(T)
print("Pre-order for node '1':")
pre_order(T, '1') #Implementation of pre_order() function is omitted, refer to the previous section0
├── 1
│ ├── 3
│ │ ├── 7
│ │ └── 8
│ └── 4
│ └── 9
└── 2
├── 5
└── 6
Pre-order for node '1':
1
3
7
8
4
9
Post-order Traversal
Post-order traversal can be thought of as the opposite of the pre-order traversal. In this mode, the left subtree and the right subtree are visited before the root, hence the name "post-order".
The traversal follows the order left -> right -> root
Consider our demo tree below;

With post-order traversal the nodes will be visited in the following order:
7, 8, 3, 9, 4, 1, 5, 6, 2, 0,
Similar to pre-order, post-order traversal can be performed on the subtree rooted at a specific node instead of the entire tree.
The post-order algorithm can be implemented recursively through the following steps:
- Recursively visit the children of the root node.
- Visit the root node.
Note that the above steps are just like in pre-order, but reversed.
implement post_order()
def post_order(T, nid):
for child in T.children(nid):
post_order(T, child.identifier)
print(T.get_node(nid).data)post_order() for entire tree
#import the Tree class
from treelib import Tree
#create a tree object
T = Tree()
#add nodes.
T.create_node(data = 0, identifier = '0')
T.create_node(data =1, identifier = '1', parent = '0')
T.create_node(data = 2, identifier = '2', parent = '0')
T.create_node(data = 3, identifier = '3', parent = '1')
T.create_node(data = 4, identifier = '4', parent = '1')
T.create_node(data = 5, identifier = '5', parent = '2')
T.create_node(data = 6, identifier = '6', parent = '2')
T.create_node(data = 7, identifier = '7', parent = '3')
T.create_node(data = 8, identifier = '8', parent = '3')
T.create_node(data = 9, identifier = '9', parent = '4')
print(T)
print("Post-order:"
post_order(T, T.root) #Implementation of post_order() function is omitted, refer to the previous section0
├── 1
│ ├── 3
│ │ ├── 7
│ │ └── 8
│ └── 4
│ └── 9
└── 2
├── 5
└── 6
Post-order:
7
8
3
9
4
1
5
6
2
0
Use another node instead of root to perform post-order traversal for the subtree rooted at that node.
Conclusion
The modes of tree traversal that we have looked at above are applicable to all type of trees. There are other modes that are only applicable to specific type of trees. One such example is the in-order traversal that can only be applied to a binary tree.
