Insertion sort implementation
def insertion_sort(lst):
for i in range(1, len(lst)):
j = i
while (j > 0) and lst[j-1] > lst[j]:
lst[j-1], lst[j] = lst[j], lst[j-1] #swap the elements
j -=1
#sort a list
L = [5, 2, 9, 3, 6, 1, 0, 7, 4, 8]
insertion_sort(L)
print("The sorted list is: ", L)
Insertion sort is a simple yet relatively efficient comparison-based sorting algorithm.
Compared to other basic sorting algorithm such as bubble sort and selection sort, insertion sort performs relatively well especially on small-to-medium and mostly sorted lists. It also has a stable sorting behavior, meaning that elements with equal values will maintain their original relative order after sorting.
Insertion sort works in-place, in that it re-arranges the elements of the original list instead of creating a new list. This makes it efficient in terms of memory usage.
Compared to other advanced sorting algorithm such as quicksort and mergesort, insertion sort is relatively easy to understand and implement. However it has an average and worst-time complexities of O(n2), this means that it can be inefficient when sorting large dataset. It works well when the input list is small in size and or it is nearly sorted.
Algorithm Description
In insertion sort, the input array/list is divided into two segments, the sorted segment on the left and the unsorted segment on the right. Initially, the sorted segment is made up of only the first element of the list, while the unsorted segment is made up of the rest of the list elements.
The algorithm iterates through the unsorted segment and takes one element at a time, comparing it with the elements in the sorted segment. It finds the correct position for the element in the sorted segment and inserts it there, shifting the other elements if necessary. The process continues until all elements in the unsorted segment are inserted into their correct positions in the sorted segment.
The following is the higher-level description of the steps in the insertion sort algorithm:
- The first element is already sorted.
- Pick the next element.
- Compare it with the the elements in the sorted segment.
- Insert it before all larger elements.
- Repeat steps 2-4 with the rest of the unsorted elements until the entire list is sorted.
Insertion sort Example
In this part we will demonstrate the steps insertion sort algorithm would follow to sort the following list.

In the first step the sorted segment is only made up of the first element of the list. Logically, a list with only one item is already sorted.

We will use color green to indicate the elements in the sorted segment and red for element in the unsorted segment.
We start by picking an unsorted element and placing it at its position in the sorted segment. The first unsorted element is 4, so we pick it and insert it at its place in the sorted segment.
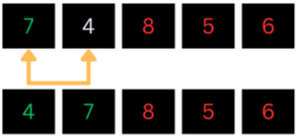
In the above case, 4 is smaller than 7 so the two are swapped. We now move on to the next unsorted element which is 8.

In the above case, we found that 8 is already sorted so no need for performing any action.
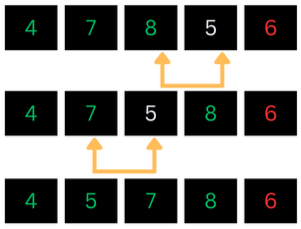
After placing 5 at its place, the unsorted segment is now only made up of a single element, 6. let us put it in its place.
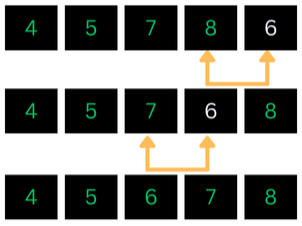
After performing the above step, we are done and the list is now sorted.
Insertion sort implementation.
We can implement insertion sort through nested loops. the first loop picks the current unsorted element and the inner loop inserts it at its place in the sorted segment. The most suitable approach of implementing this is by use of an outer for loop and an inner while loop.
def insertion_sort(lst):
for i in range(1, len(lst)):
j = i
while (j > 0) and lst[j-1] > lst[j]:
lst[j-1], lst[j] = lst[j], lst[j-1] #swap the elements
j -=1
#sort a list
L = [99, 9, 0, 2, 1, 0, 1, 100, -2, 8, 7, 4, 3, 2]
insertion_sort(L)
print("The sorted list is: ", L)The insertion_sort() function above, does not return any value because the input list is being sorted in-place.
For loops are useful when we know in advance the number of iterations needed and in contrast, while loops are more suitable in cases where we do not know in advance the number of iterations to be performed. The fitness of each of the two loops is clearly shown in the above implementation of insertion sort. Using an inner while loop ensures that we can efficiently get out of the loop after the element is placed at its position without using extra conditional checks.
Descending insertion sort
To sort the list elements in descending order using insertion sort, we simply need to change a single statement in the insertion_sort() function and actually just a single character.
Changing the > character in the second condition of the while loop to < character will make the algorithm to sort the elements in descending order i.e we need to change the statement from while (j > 0) and lst[j-1] > lst[j]: to while (j > 0) and lst[j-1] < lst[j]:.
descending insertion sort
def insertion_sort(lst):
for i in range(1, len(lst)):
j = i
while (j > 0) and lst[j-1] < lst[j]: #changed > to <
lst[j-1], lst[j] = lst[j], lst[j-1] #swap the elements
j -=1
#sort a list
L = [99, 9, 0, 2, 1, 0, 1, 100, -2, 8, 7, 4, 3, 2]
insertion_sort(L)
print("The sorted list is: ", L)Algorithm analysis
The running time complexities of insertions sort are as shown below:
- best case -
O(n), this is when the list is already sorted. - Average case -
O(n2), this is when the list is randomly sorted. - Worst case -
O(n2), When the list is reverse sorted.
Applications of insertion sort
The following list outlines cases where insertion sort may be suitable:
- When the dataset is not very large in size.
- When the elements are almost sorted.
- When simplicity and stability are needed.
Insertion sort is relatively more performant compared to other basic sorting algorithm such as bubble sort or selection sort. However, its O(n2) average and worst running time makes it limited compared to other sorting algorithms such as quicksort or mergesort. It is, therefore, more suitable when sorting small sets of data.
