Implement bubble sort algorithm in Python

#Optimized bubble sort
def bubble_sort(lst):

  swapped = True
  while swapped == True:
    swapped = False
    for j in range(len(lst)-1):  
      
      if(lst[j]>lst[j+1]):
        lst[j], lst[j + 1] = lst[j + 1], lst[j] #swap the elements
        swapped = True

#sort a list
L = [9, 0, 2, 1, 0, 1, 100, -2, 8, 7, 4, 3, 2]

bubble_sort(L)  
print("The sorted list is: ", L)

Bubble sort is the most basic sorting algorithm. Its simplicity makes it suitable for introducing computer science students to sorting algorithms. However, it has an average and worst case running time of O(n2), making it highly inefficient for sorting medium to large dataset.

Bubble sort is highly limited compared to other sorting algorithms and, therefore,  not suitable for practical environments beyond educational ones. 

Despite its limitations, understanding the operation of bubble sort is essential for you to understand how more advanced sorting algorithms works.

In the following parts we will understand how the bubble sort algorithm operates and how to implement it in Python.

Bubble sort Algorithm description

In bubble sort algorithm, each pair of adjacent elements are compared and only swapped if they are not in order. That is , if the first element in the pair is larger than the other element, the elements are swapped.

The swapping of elements happens in-place meaning that the original list gets modified.

If we have a list of n elements, the bubble sort algorithm can be performed through the steps shown below:

With the above steps,  the largest elements gradually moves to the end of the list until the list is sorted.

Sorting Example

Consider if we use bubble sort to sort the following list:

In the first step the largest value which is 6 will move to the end of the list as shown below:

Similarly the second largest value will move to the second to last position;

Note that in the above step, 4 and 5 are already sorted and therefore, the swap operation is not performed.

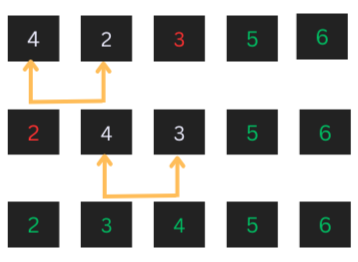
After performing the above step, where 4 moves at its position at the back of the list, the list become sorted.

Direct Implementation

To implement bubble sort, you can use nested loops, the following example shows how we can achieve this with for loops:

def bubble_sort(lst):

  for i in range(len(lst)-1):
    for j in range(len(lst)-1):  

      if(lst[j]>lst[j+1]):
        lst[j], lst[j + 1] = lst[j + 1], lst[j] #swap the elements

#sort a list
L = [9, 0, 2, 1, 0, 1, 100, -2, 8, 7, 4, 3, 2]

bubble_sort(L)  
print("The sorted list is: ", L)

The bubble_sort() function does not return any value because the sorting happens to the original list.

As show in the above example, nested for loops provides a much direct way of implementing the bubble sort algorithm, but we can also use nested while loops to achieve the same, as shown below.

def bubble_sort(lst):

  i = 0
  while i <  len(lst):
    j = 0
    while j < len(lst)-1:
      if(lst[j]>lst[j+1]):
        lst[j], lst[j + 1] = lst[j + 1], lst[j]
      j += 1
    i += 1

L = [9, 7, 1, 2, 4, 1, 3, 0, 6, 5, 8]
bubble_sort(L)  
print("The sorted list is: ", L)

Optimized Implementation

The previous implementation of bubble sort has one avoidable performance inefficiency. This is because whether the list is already sorted, not sorted or reverse sorted, the algorithm still finishes with the worst-case running time of O(n2).

Note that if the algorithm moves through the entire list without performing the  swap operation on any pair of elements, it means that the list is already sorted. We can, therefore, optimize bubble sort to avoid performing unnecessary comparisons by defining an intermediate variable to check whether a swap operation has taken place or not.

def bubble_sort(lst):

  swapped = True
  while swapped == True:
    swapped = False
    for j in range(len(lst)-1):  
      
      if(lst[j]>lst[j+1]):
        lst[j], lst[j + 1] = lst[j + 1], lst[j] #swap the elements
        swapped = True

#sort a list
L = [9, 0, 2, 1, 0, 1, 100, -2, 8, 7, 4, 3, 2]

bubble_sort(L)  
print("The sorted list is: ", L)

Optimized bubble sort has a best case running time of O(n), this is is when the list is already in a sorted state. It still has an average and worst case running time of O(n2).

Bubble sort's space and time complexity

space complexity

Bubble sort has a space complexity of O(1) this is because no extra lists are used in its internal logic. The sorting happens directly on the input list without the use of intermediate lists.

Time complexity

The unoptimized version of bubble sort has a time complexity of O(n²) regardless of whether the input list is already sorted, not sorted or reverse sorted. 

On the other hand, the time complexity cases of the optimized version are as highlighted below:

• Best-O(n) - This happens when the input list is already sorted as we simply traverse through the list once.
• Average-O(n²) - When the input list is not sorted and the elements are in arbitrary order.
• Worst-O(n²) - When the input list is reverse sorted and, therefore, the swap operation happens with every comparison.

When to use bubble sort

Bubble sort is suitable in the following cases:

1. When sorting small datasets
2. When complexity does not matter.
3. When small and concise code is required.