Binary Trees in Python

A binary tree is  a type of tree where each node has at most two child nodes. The two children are usually referred to as left and right child.

Normally, an internal node looks as follows.

Binary trees starts with a root node, which is the topmost node, and the other nodes branch of from this node in a hierarchical manner.

The following is an example of a binary tree.

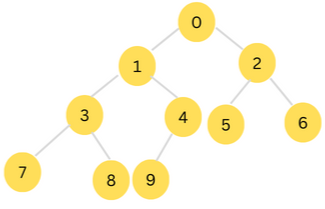
A subtree branching off from the left child of a given node, is referred as its left subtree, and similarly, a right subtree is the subtree that branches off from the right child.

Balanced vs Unbalanced Binary Trees

A binary tree can be balanced or unbalanced.  

In a balanced binary tree  the difference in the height of the left and right subtrees of any node is no more than one. This means that the nodes in the tree are almost evenly distributed, with roughly the same number of nodes on each side.

Example of a balanced binary tree.

In contrast, in unbalanced binary tree the difference in height between the left and right subtrees of any node can be greater than one. This creates an uneven distribution of nodes, with one side being significantly longer than the other.

Example of unbalanced binary tree

Note that in the tree shown above, the node with a value of 9 has no left subtree(height 0),  but the right subtree has a height of 2. This makes the entire tree unbalanced.

Balanced binary trees have some advantages over unbalanced ones especially if the tree is large. For example, searching, insertion and deletion operations can be performed optimally on balanced trees, as the height of the tree is minimized, reducing the number of comparisons needed to access a node.

Perfect vs imperfect binary trees

In a perfect binary tree all internal nodes have two child nodes, and all leaf nodes are at the same level. This means that every level of the tree is completely filled, and the number of nodes doubles at each level.

Logically, a perfect binary tree is balanced.

Example of a perfect binary tree

In an imperfect binary tree the number of child nodes for each internal node can vary. This means that some levels of the tree might not be completely filled, and the number of nodes may not double at each level.

Implementing the Node class

In addition to the stored element, a node in a binary tree usually contains 3 more fields to store its relationship to its parent node, its left child, and its right child. 

When implementing a binary tree,  the Node class can be implemented as follows:

class Node:
   def __init__(self, value = None, parent = None, left = None, right = None):
        self.value = value
        self.parent = parent
        self.left = left
        self.right = right

The binarytree module

The standard library does not provide an implementation of a binary tree, we can implement the class from scratch using OOP or use third party libraries.

There are several third-party libraries and modules that offer implementations of binary trees, binarytree is one such module. The module allows us to create, visualize and manipulate binary trees with ease.

We will first have to install the module in our program, using the following pip command.

pip install binarytree

binarytreee.Node class

The Node class  represents a node in a binary tree, it has the following syntax.

binarytree.Node(value, left = None, right = None)

If either right or left arguments are not instances of the binarytree.Node class, a NodeTypeError exception will be raised.

from binarytree import Node

root = Node(5) #the root node.
root.left = Node(4) 
root.right = Node(6)
print(root)

As you can see from the above example, the module uses pretty-printing making it easy to understand the relationship between the nodes. 

We can use the properties() method of node objects to view the properties of a given node. The method returns a dictionary  containing the properties of the node.

from binarytree import Node

root = Node(5) #the root node.
root.left = Node(4) 
root.right = Node(6)
print(root)

#get the properties
print("Properties of node 'root': ")
for k, v in root.properties.items():
    print(k, ':', v)

The following example shows a more elaborate node relations.

from binarytree import Node

#create the nodes
root = Node(5) #the root node.
n1 = Node(4) 
n2 = Node(6)
n3 = Node(3)
n4 = Node(7)
n5 = Node(2)
n6 = Node(8)

#define the relationships between them
root.left = n1
root.right = n2
n1.left = n3
n1.right =n5
n2.left = n4
n2.right = n6

print(root)

Build a binary tree with pre-filled random values 

The tree class in the binarytree module  allows us to create a binary tree with pre-filled random values. We just need to specify the height of the tree and some other properties, if necessary.

binarytree.tree(height = 3, is_perfect = False, letters = False )

from binarytree import tree

T = tree()
print(T)

In the above example, we created an imperfect binary tree with a height of 3. In the following example, we use letters as values instead of numbers.

from binarytree import tree

T = tree(height = 3, is_perfect = True, letters = True)
print(T)

Build a binary tree from iterables

The build() method in the binarytree module creates a binary tree from an iterable containing the tree elements arranged in breadth-first order.

In the breadth-first order, the elements are arranged in height/level-order, meaning the root is the first element, followed by the elements at the next level, and so on.

import binarytree

#elements stored in breadth-first order
elements = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]#list

#create the tree
BT = binarytree.build(elements)
print(BT)

We can use any other type of iterable such as tuples, sets, range, etc.

Binary Tree Traversal

There are four main modes of traversing a binary tree.

Trees and Nodes created from binarytree modules keeps four lists in which the nodes are arranged for the respective traversal mode. The four lists are, levelorder, inorder, preorder and postorder.

from binarytree import tree

T = tree(is_perfect = True)
print(T)

print("Level order traversal:")
for node in T.levelorder:
    print(node.val, end = ' ')

from binarytree import tree

T = tree(is_perfect = True)
print(T)

print("Inorder traversal:")
for node in T.inorder:
    print(node.val, end = ' ')

from binarytree import tree

T = tree(is_perfect = True)
print(T)

print("Preorder traversal:")
for node in T.preorder:
    print(node.val, end = ' ')

from binarytree import tree

T = tree(is_perfect = True)
print(T)

print("Postorder traversal:")
for node in T.postorder:
    print(node.val, end = ' ')