Recursion in Python

Recursion is a process where a function calls itself directly or indirectly. It is a powerful programming technique which makes it possible to express operations in terms of themselves.

Recursion like loops,  allows us to achieve repetition, however, the internal working between loops and recursion is entirely different. 

In Python, a function is recursive if it is defined to call itself either directly or indirectly through another function within its body. Well, what does that mean ?, let me start by showing you a bad example to demonstrate recursion:

def  func():
    func()

The reason why the above is a bad example is because if you run the above function it would never terminate normally . I only wanted to show you what we mean by a function calling itself. The closest thing to the above example is an infinity loop.

Indirect recursion is when a function is called by another function within its body, example:

def func1():
    #statements
    func2()

def func2():
    #statements
    func1()

func1()

Define recursive functions that terminate

We will start with a working example before describing what is going on.

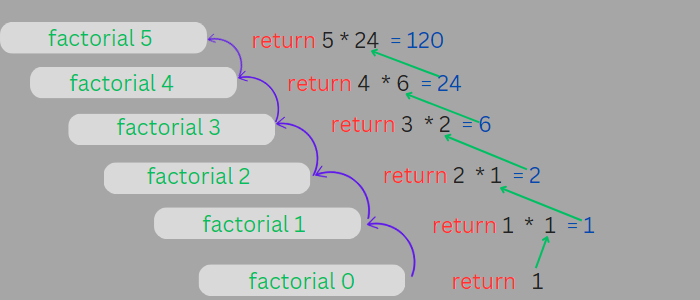
The factorial of a given number is the product of all positive integers less than or equal to the given number. For example, the factorial of 5 is 5 x 4 x 3 x 2 x 1 = 120. You should note that we can find the factorial of 5 by multiplying the factorial of 4  by 5 i.e 5 x (4 x 3 x 2 x 1) = 5 x 24 , in the same way that we can find the factorial of 4 by multiplying the factorial of 3 with 4 i.e 4 x (3 x 2 x 1) = 4 x 6 = 24, and so on. Recursive functions utilize the same principle in order to  compute a value cumulatively from smaller solutions.

The following function shows a recursive function to calculate the factorial of a number:

def factorial(n):
   if n == 0:
      return 1
   else:
      return n * factorial(n - 1)

factorial(5)
//120

First and foremost, all recursive functions should have a base case in order for the function to terminate. The base case is the simplest case of a given problem that can be used as the starting point for an inductive argument, it is responsible for the function's termination. During each recursion trace, the function advances closer and closer to the base case, until the base case is met stopping the recursion. Any recursive function which does not define a base case will not terminate normally. In our above example, the base case is met when the value of n becomes 0.  

To understand better how recursive functions work, you first need to be conversant with how functions work at low-level. Whenever a function is called in Python, a stack frame is created in the memory to store the parameters and local variables of the function. When the function returns, the stack frame is removed from the memory. Recursive functions work in a similar way, except they don't get removed from the stack after they return. Instead, they stay on the stack until their recursive calls have finished executing. Whenever a recursive call is made, a new stack frame is added to the stack, until all the recursive calls have finished and the initial call can be resolved. This keeps happening until the base case of the function is reached and the stack frames can be popped off one by one. The following image demonstrates the recursion trace for the factorial function:

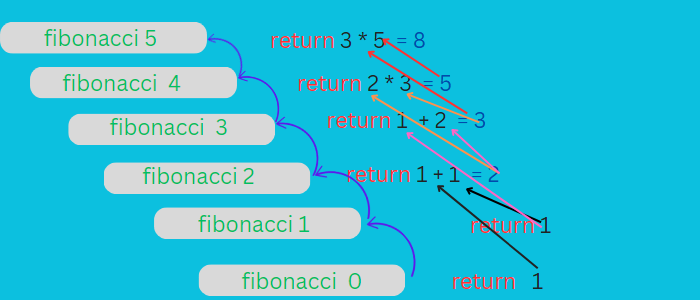
Recursion in the Fibonacci sequence 

The Fibonacci series is a sequence of numbers in which each number is the sum of the two preceding numbers, starting from 0 and 1. So the first few numbers in the series are: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

Recursive function to get the nth number in the Fibonacci series:   

def fibonacci(n):
   if n <= 1: 
       return n
   else:
       return( fibonacci(n-2) + fibonacci(n-1))

fibonacci(1)
//1
fibonacci(4)
//3
fibonacci(7)
//13

In the above case, the base case is reached if n is less than or equal to 1.

The following example demonstrates the recursion trace for Fibonacci function with n as 5:

Use recursion to detect palindromes

A palindrome is a word or phrase that is the same forward as it is backward. Meaning that  if the word or phrase is read from left to right, the same sequence of letters and words appears from right to left as well. Some examples of palindromes include "racecar", "madam", "level", etc.

The following example uses recursion to tell whether a word is a palindrome or not, it returns True if so and False otherwise.  

def is_palindrome(word): 
    if len(word) <= 1: 
       # Base case 
       return True

    if word[0] != word[-1]:
        #Another Base case
        return False
     
    # Recursive call
    return is_palindrome(word[1:-1])

# Tests
print(is_palindrome('racecar'))
print(is_palindrome('wow'))
print(is_palindrome('level'))


print(is_palindrome('hello')) 

The is_palindrome()  function above takes a single string argument and checks if it is a palindrome. It starts with two base cases. If the length of the word is less than or equal to 1, then it is a palindrome. If the first letter of the word is not equal to the last letter, then it is not a palindrome. For all other words, it checks if the first and last letters are equal and then calls itself with the word to repeat the process. The word argument is sliced to omit the first and last characters on each recursive call until either of the base cases is reached. 

Recursion for traversing irregularly nested sequences

In cases where we are traversing a sequence, loops such as for and while  work well when the  level of nesting in the sequence is regular, for example   we can use  nested for loop to traverse a regularly nested list such as [[1, 2], [3, 4], [5, 6, 7], [ 8, 9],  [10, 11]]

L = [[1, 2], [3, 4], [5, 6, 7], [ 8, 9], [10, 11]]

for i in L:
   for j in i:
        print(j)

However, when the level of nesting becomes slightly irregular it becomes almost impossible to use loop in traversing the sequence. For example in    [[[1, 8, 9], [4, 6], [3, 2, 5]], [[7, 0], [4, 2, 6], [1, 3, 9]]]. 

This is one area  where recursive functions triumph over loops.

def myfunc(lst):
    
    for element in lst:
        if isinstance(element, list):
           #the recursive call
           myfunc(element)
        else: 
           print(element)

my_list = [[[1, 8, 9], [4, 6], [3, 2, 5]], [[7, 0], [4, 2, 6], [1, 3, 9]]]

myfunc(my_list)

The function iterates through each element, if the element is a list, it calls itself recursively, if the element is not a list, it prints out the element.

Maximum Recursion Depth

Maximum recursion depth is the maximum number of times a function can call itself before Python raises a RecursionError. The default recursion limit in Python is usually set to 1000, but this limit can be updated depending on the needs of the program.

Typically, when a recursive function is called without a base case, it will keep calling itself indefinitely until the maximum recursion depth is reached. Example:

def func():
    func()

func()
//RecursionError: maximum recursion depth exceeded

We can use the sys.getrecursionlimit() function to check the current maximum recursion depth.

import sys
print(sys.getrecursionlimit())
//1000

To increase or decrease the limit, we can use sys.setrecursionlimit() function with the prospective limit as the argument. Example:

import sys
sys.setrecursionlimit(2000)
print(sys.getrecursionlimit())
//2000

However, it is not recommended to set the recursion limit too high as it can lead to stack overflow errors and cause your program to crash. Instead, you write your code in a way that avoids deep recursion if possible, or use other techniques such as iteration.

Common Uses of Recursion

Some computational tasks are naturally solved better using recursion. Some common such tasks includes:

Implementations of the above algorithms is beyond the scope of this article.

Downsides of using recursion

While recursion can be an efficient and powerful way of solving certain types of problems , it does have a large resource footprint. It requires creating a 'stack' of all the recursive calls, which requires additional memory and processor time. Recursive algorithms also tend to take up more memory as compared to iterative algorithms that solve the same problem.  It is, therefore, a good programming practice to avoid using recursion in cases where it would be more straightforward to use loops. For example, the following is a recursive function to print integers from 1 to integer i:

def printNums(i):
    if i == 0:
       return
    printNums(i-1)
    print(i)

printNums(9)
//1
//2
//3
//4
//5
//6
//7
//8
//9

Using recursion in cases like the one shown above is unnecessarily complex, and should be avoided.

Apart from being memory intensive, other downsides of recursion includes: