Implement Stack data structure in Python

Stack is a linear data structure that follows the Last In First Out (LIFO) principle, where the last element inserted is the first one to be removed. 

The name "stack" is  derived from the analogy of a stack of plates, books, etc. Imagine a stack of plates where you can only take the topmost plate, and you can only add new plates on the top. This is essentially how a stack works.

The stack is probably the simplest data structure, however, it is also one of the most commonly used ones. Ever used the "undo" feature in your text editor?, or  used your calculator to solve a complex math expression? Well, that's thanks to a stack!.

In this article, we'll look on various ways to implement stacks,  how they work and some common applications.

Stack abstract data type

An abstract data type(ADT) is a description of the behavior of a data structure without the actual implementation. In this part we will look at the behavior of a stack and the operations it supports. 

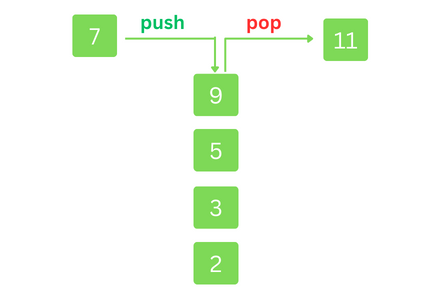
Main operations on a stack only happens at one end, which is referred to as the 'top of the stack'. 

The two main operations on a stack are push and pop. Push operation adds an item to the top of the stack, and pop removes an item from the top of the stack. 

Formally, a stack should support the following operations/methods:

stack implementation

In this section, we will implement a class to model a stack. A list will be used  as the internal container for storing the stack elements.

#an exception to be raised by an empty stack
class EmptyStack(Exception):
    pass

class Stack:
    
    def __init__(self):
        self._items = [] #non-public list for storing stack elements

    def __len__(self):
        return len(self._items)

    def isEmpty(self):
        return len(self) == 0 

    def push(self, e):
        self._items.append(e) #add the element at the end of the list

    def top(self):
        if self.isEmpty():
            raise EmptyStack("Stack Is Empty.")
        return self._items[-1] #Return the last element in list

    def pop(self):
        if self.isEmpty():
            raise EmptyStack("Stack Is Empty.")
        return self._items.pop() #pop the last item from the list

# test the stack
S = Stack()

S.push("A")
S.push("B")
S.push("C")
print(S.pop())
print(S.pop())
print(S.pop())
print(S.pop())
 Visualize 
copycopied!

Output:
C
B
A

Traceback (most recent call last):
  File "<string>", line 38, in <module>
  File "<string>", line 26, in pop
EmptyStack: Stack Is Empty.

[Finished in 0.01065357867628336s]

In the above snippet, we implemented the Stack classes with the methods to support the various stack operations. The __len__() method allows us to get the size of the stack using the len() function.

We used some examples to demonstrate the push() and pop() methods , you can experiment more with the rest of the methods on your own.

Using a list directly as a Stack

One obvious thing that I didn't mention in the previous section is that you can use a list directly to simulate a stack. This is because I wanted to  focus on the concept of a stack as an abstract data type, rather than just using the built-in structures. The Stack class as we defined it in the previous section is more intuitive and higher-level than directly using a list. 

The list supports operations that allows it to be used as a stack. With this approach,  `append()` and `pop()` methods of a list  are used to simulate the `push()` and `pop()` operations of a stack, respectively. 

S = []

#add elements
S.append(10)
S.append(20)
S.append(30)
S.append(40)
S.append(50)

#Get the size of the stack
print("Size: ", len(S))
print(S)
#remove elements
print(S.pop())
print(S.pop())
print(S.pop())
print(S.pop())
print(S.pop())
print(S)
print(S.pop())

 Visualize 
copycopied!

Output:
Size:  5
[10, 20, 30, 40, 50]
50
40
30
20
10
[]

Traceback (most recent call last):
  File "<string>", line 20, in <module>
IndexError: pop from empty list

[Finished in 0.010432448238134384s]

The queue.LifoQueue class

The queue module in the standard library defines the LifoQueue class which provides a more efficient implementation of a Stack. The greatest advantage the LifoQueue class is that it is thread-safe, this allows multiple threads to access the same stack without causing any issues or conflicts. 

This LifoQueue is a typical  stack, it supports all the stack operations through the following methods.

#import the LifoQueue class
from queue import LifoQueue

S = LifoQueue()
#push elements
S.put(10)
S.put(20)
S.put(30)

#the size of the stack
print("Size: ", S.qsize())
#pop elements
print(S.get())
print(S.get())
print(S.get())
 Visualize 
copycopied!

Output:
Size:  3
30
20
10

Uses of Stack

Stacks have a lot of application in modern software development. In this section, we will focus on some basic ways that stacks are applied.

Reversing data

We can use a stack to easily reverse data. For example, assume you want to reverse the lines in a text file. You can read the data into a stack, then pop each element of the stack and write it back to the file.

#the Stack implementation is omitted
S = Stack()

#open the file for read
with open("myfile.txt", 'r') as file:
    for line in file:
         S.push(line)

#open the file for write
with open("myfile.txt", 'w') as file:
    while not S.isEmpty(): #write until the stack is empty
         file.write(S.pop()) #write to the file
 Visualize 
copycopied!

Matching brackets and other delimiters

Assume you want to check whether an expressions with various type of  brackets is correctly formatted and that each opened bracket is closed, as in   (5 + [4 * (7 - 2)]).

We can push each opening bracket into the stack and whenever we encounter its closing counterpart, we pop it from the stack. If by the end the stack is empty, we can conclude that the expression is correctly formatted.

#stack implementation is omitted

def is_matched(exp):
    opening = "([{"
    closing = ")]}"
    S = Stack()
    for i in exp:
        if i in opening: S.push(i)
        elif i in closing: 
            if S.isEmpty(): return False
            if closing.index(i) != opening.index(S.pop()): return False 

    return len(S) == 0
    
#test the is_matched function
print(is_matched("(1 + 2)+ (3 - 6)"))
print(is_matched("(1 + 2)+ [3 - 6)"))
print(is_matched("(1 + 2)+ (3 - 6"))
print(is_matched("{1 + 2}+ {3 - 6}"))
 Visualize 
copycopied!

Output:
True
False
False
True

Implementing undo/redo functionality

One of the most common uses of stack is to implement undo/redo functionality in applications. Each time a user performs an action, the action is added to the stack. If the user wants to undo an action, the most recent action is popped off the stack. If they want to redo an action, the previously popped action is pushed back onto the stack.

Managing function calls

In programming languages like Python, when a function is called, the current state of the program is saved on the stack. The function is then executed and once it is finished, the state is restored by popping it off the stack. This allows for nested function calls and recursion to work efficiently.