Implement Merge-Sort in python

#merge sort

#the merge algorithm
def merge(L1, L2, L):
  i = 0
  j = 0
  while i+j < len(L):
    if j == len(L2) or (i < len(L1) and L1[i] < L2[j]):
       L[i+j] = L1[i]
       i += 1
    else:
       L[i+j] = L2[j]
       j += 1

#main function
def merge_sort(L):

  n = len(L)
  if n < 2:
     return # list is already sorted

  # divide
  mid = n // 2 #midpoint
  L1 = L[0:mid] # the first half
  L2 = L[mid:n] # the second half
 
  # conquer with recursion
  merge_sort(L1) # sort first sub-list
  merge_sort(L2) # sort second sub-list

  # merge result
  merge(L1, L2, L) 

#example
L = [7, 5, 1, 4, 2, 8, 0, 9, 3, 6]
print('Before: ', L)
merge_sort(L)
print('After: ', L)

The merge sort algorithm uses the divide and conquer technique to efficiently sort a list of elements.

Divide and conquer involves breaking down a larger problem into smaller more manageable sub-problems, solving the sub-problems and then merging their solutions to solve the original problem.  In the case with merge-sort, the algorithm breaks down the list into smaller sub-lists, sorts those sub-lists recursively, and then merges the sorted sub-lists back together until the entire list is sorted

Merge sort has  time complexity of O(nlogn) in both average and worst case scenarios, this makes it one of the fastest sorting algorithms and consequently, one of the most sought after.

Merge sort is stable, meaning that it preserves the relative order of equal elements in the original list.

Algorithm Description

Assuming we have a list L, the basic steps followed by merge sort are as highlighted below:

Example

Consider if we want to sort the following list using merge sort.

In the first step of merge sort, the list will be recursively divided into individual sub-lists. This means that the list will be split into two sub-lists and then each of the sub-lists will be split into two more sub-lists, and so on until each sub-list contains only a single element. The following figure demonstrates the splitting phase:

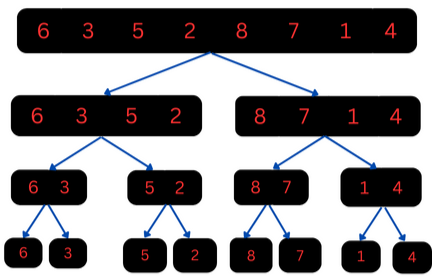
After the divide step is over, we need to recursively sort each sub-list and then merge it with the other sorted sub-lists. This is known as the "conquer" step. 

The conquer step can be visualized as starting from the bottom level moving upwards,  sorting and combining the sub-lists at each level until the entire list is sorted.

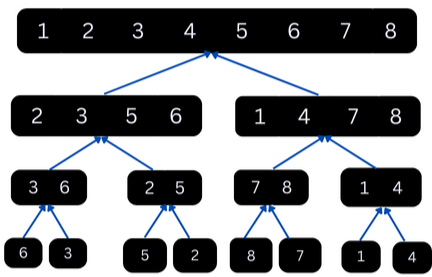
As shown in the above figure, at the beginning of the conquer step(at the bottom level), each sub-list is made up of a single element. Logically, a list with only one element is already sorted. Sub-lists with more than a single elements in upper levels are first sorted before they are merged with the other sub-lists.

Merge sort implementation

In this section, we will implement the merge sort algorithm using functions.

For the sake of clarity, we will split the algorithm into two functions,  merge() and merge_sort(). The merge() function will be responsible for combining two already sorted sub-lists into a single sorted list. The merge_sort() function is where the main logic of the algorithm will go.

#L is the list while L1 and L2 are the sublists.

def merge(L1, L2, L):
  i = j = 0
  while i+j < len(L):
    if j == len(L2) or (i < len(L1) and L1[i] < L2[j]):
       L[i+j] = L1[i]
       i += 1

    else:
       L[i+j] = L2[j]
       j += 1

#example
L = [2, 7, 4, 0, 6, 5]
L1 = [2, 4, 7]
L2 = [0, 6, 5]

merge(L1, L2, L)
print(L)

The merge() function above takes in two sorted sub-lists(L1 and L2) and puts their elements back to the original list(L) in a sorted state. It does so by determining from which sub-list the next item should be taken before inserting the picked item back to list L. For clarity, let us look at the function statement by statement:

 After implementing the merge() function, the implementation of the merge_sort() function become easier.

#the implementation of merge() is omitted, refer to the previous snippet.

def merge_sort(L):

  n = len(L)
  if n < 2:
     return # list is already sorted

  # divide
  mid = n // 2 #midpoint
  L1 = L[0:mid] # the first half
  L2 = L[mid:n] # the second half
 
  # conquer
  merge_sort(L1) # recursively sort first sub-list
  merge_sort(L2) # recursively sort second sub-list

  # merge
  merge(L1, L2, L) 

#usage example
L = [99, 9, 0, 2, 1, 0, 1, 100, -2, 8, 7, 4, 3, 2]
merge_sort(L)
print(L)

The merge_sort() function does not return any value because the sorting happens to the original list.

The entire merge sort implementation is as shown below:

#merge sort implementation

def merge(L1, L2, L):
  i = 0
  j = 0
  while i+j < len(L):
    if j == len(L2) or (i < len(L1) and L1[i] < L2[j]):
       L[i+j] = L1[i]
       i += 1
    else:
       L[i+j] = L2[j]
       j += 1

def merge_sort(L):

  n = len(L)
  if n < 2:
     return # list is already sorted

  # divide
  mid = n // 2 #midpoint
  L1 = L[0:mid] # the first half
  L2 = L[mid:n] # the second half
 
  # conquer with recursion
  merge_sort(L1) # sort first sub-list
  merge_sort(L2) # sort second sub-list

  # merge result
  merge(L1, L2, L) 

#usage example
L = [99, 9, 0, 2, 1, 0, 1, 100, -2, 8, 7, 4, 3, 2]
merge_sort(L)
print(L)

Complexity analysis

The time complexities of merge sort with a list of size n, are as outlined below:

• Best case - O(nlogn) , this happens when the input list is already sorted.
• Average case - O(nlogn), when the input list is randomly sorted.
• Worst case - O(nlogn), when the input list is reverse sorted.

Space complexity

Merge sort has a space complexity of O(n) due to the space occupied by the sub-lists.