Implement Queue data structure in Python

The queue is one of the most fundamental data structures. 

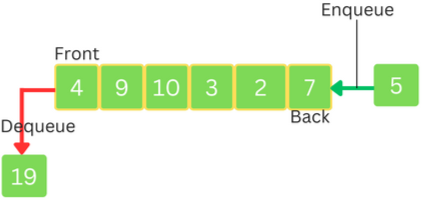
A queue observes the First-In-First-Out (FIFO) principle, where the first element inserted is the first one to be removed. The structure can be visualized as in a line of people waiting for a service, where the person who enters first is served first.

The Queue Abstract Data Type

A Queue have two main operations, enqueue and dequeue. The enqueue operations adds an elements at the rear end of the queue, while  the dequeue operation removes the element at the front of the Queue.

Altogether, a queue should support the following operations.

List-based Queue implementation

We will first look on how to implement a Queue class from scratch to better understand its mechanisms before exploring better built-in implementations. 

We will implement the Queue class with a list as the underlying structure for storing the queue elements.

#exception to be raised by an empty queue
class EmptyQueue(Exception):
   pass

class Queue:
   def __init__(self):
         self._data = [] #a non-public list for storing the elements
 
   def __len__(self):
        return len(self._data)

   def is_empty(self):
      return len(self) == 0

   def first(self):
      if self.is_empty():
         raise EmptyQueue("Queue is empty, can't dequeue")

      return self._data[-1]

   def enqueue(self, e):
      self._data.append(e)

   def dequeue(self):
      if self.is_empty():
         raise EmptyQueue("Queue is empty, can't dequeue")
      return self._data.pop(-1) #This operation is very inefficient.

#test the queue
Q = Queue()
Q.enqueue("Python")
Q.enqueue("Java")
Q.enqueue("C++")
Q.enqueue("Ruby")

print(len(Q))
print(Q.dequeue())
print(Q.dequeue())
print(Q.dequeue())
print(Q.dequeue())
print(Q.dequeue())

While the Queue class above serves as a simple and intuitive example, it is not meant for use beyond simple learning projects due to the aforementioned inefficiency. In the following parts we will discuss more robust and efficient implementations of the queue data structure.

Using collections.deque

The collections module in the standard library defines the deque class, pronounced as "deck" which offers very efficient insertion and deletion operations on either ends. We can use this class to create LIFO queues for  use even in a production setup.

The deque class have various methods, we will only discuss the ones that enables us to use it as a FIFO queue.

#import the deque class
from collections import deque

#create a queue
q = deque()

#enqueue elements 
q.append(10)
q.append(20)
q.append(30)

#the size
print("Size: ", len(q))

#dequeue elements
print(q.popleft())
print(q.popleft())
print(q.popleft())
print(q.popleft())

Since deque objects supports efficient insertions and deletions from either end, we can also add elements at the front(left) end and remove them from the back(right) end, without any change in functionality or performance. This way we can use the following methods:

#import the deque class
from collections import deque

#create a queue
q = deque()

#enqueue elements 
q.appendleft(10)
q.appendleft(20)
q.appendleft(30)

#the size
print("Size: ", len(q))

#dequeue elements
print(q.pop())
print(q.pop())
print(q.pop())
print(q.pop())

The queue module

The  queue module in the standard library also provides an efficient implementation of the queue data structure. This implementation is optimized for performance and is thread-safe. The class is more suitable for use with multi-threaded applications, as it allows multiple threads to safely insert and remove items from the queue without causing any conflicts or errors.   

The Queue class in the module defines the following basic methods.

#import the Queue class
from queue import Queue

#create a queue object
q = Queue()

#enqueue items
q.put(10)
q.put(20)
q.put(30)
q.put(40)

#get the size
print("Size: ", q.qsize())

#dequeue items
print(q.get())
print(q.get())
print(q.get())
print(q.get())