Heaps are a type of a binary trees that satisfy the heap property, which states that the key of any node is less(or greater) than the keys of its children. Any collections of elements in which the heap property is maintained can be said to form a heap.
One important resulting property of heaps is that the root node always contains the smallest value in the tree.
The figure shown below shows a min-heap.
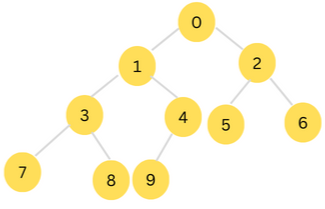
Note that every node in the tree has a value that is less than both those of its child nodes.
The heapq module in the standard library provide an implementation of heap-based priority queues. Rather than implementing a priority queue class, the module provides functions that operate on standard lists as heaps. The various functions defined in the module are as shown below;
| function | description |
|---|---|
heapify(x) |
Transforms list x into a heap, in-place, in linear time. |
heappush(h, v) |
Adds value v onto the heap h, while maintaining the heap property. |
heappop(h) |
Removes and returns the smallest item from the heap h, while maintaining the heap invariant. |
heappushpop(h, v) |
Combines the functionality of heappush() and heappop() functions. |
heapreplace(h, v) |
Removes and returns the smallest item from the heap h, and also pushes the new item v, while maintaing the heap property.. |
merge(*iterables) |
Merge multiple sorted iterables into a single sorted iterator object. |
nlargest(n, iterable) |
Returns a list with the n largest elements from the dataset defined by iterable. |
nsmallest(n) |
Returns a list with the n smallest elements from the dataset defined by iterable. |
Creating a heap with a list
The heapq.heapify() is an in-place algorithm that rearranges the elements of the list in such a way that it is organized as a heap. After the transformation, the smallest element is always at the top of the heap.
heapify a list
#import the module
import heapq
L = [3, 0, 2, 5, 1, 6, 4]
#heapify L in-place
heapq.heapify(L)
print(L)Inserting elements into the heap
Various methods such as heappush() can be used to insert elements into the heap. The insertion process happens while at the same time, the heap property is maintained.
insert elements into the heap
#import the module
import heapq
L = [3, 0, 2, 5, 1, 6, 4]
heapq.heapify(L)
heapq.heappush(L, -1)
heapq.heappush(L, 7)
heapq.heappush(L, 8)
print(L)Accessing elements from the heap
The heappop() function removes and returns the smallest element in the heap. An IndexError is raised if the heap is empty.
remove the smallest element from the heap.
#import the module
import heapq
L = [3, 0, 2, 5, 1, 6, 4]
heapq.heapify(L)
print(heapq.heappop(L))
print(heapq.heappop(L))
print(heapq.heappop(L))
print(heapq.heappop(L))
print(heapq.heappop(L))
print(heapq.heappop(L))
print(heapq.heappop(L))In the following example, we use the heapreplace() function to remove the smallest element and add another element simultaneously
#import the module
import heapq
L = [3, 0, 2, 5, 1, 6, 4]
heapq.heapify(L)
print(heapq.heapreplace(L, -10))
print(heapq.heapreplace(L, 0))
print(heapq.heapreplace(L, 10))
print(heapq.heapreplace(L, 20))
print(L)Largest and Smallest values in a heap
The two utility functions nlargest() and nsmallest() are used to get the largest and smallest values, respectively.
nlargest
import heapq
data = [6, 17, 3, 11, 13, 7, 9, 4, 8, 10]
print(heapq.nlargest(5, data))
print(heapq.nsmallest(5, data))Combine sorted iterables
The heapq.merge() is a generator function which takes multiple sorted iterables and produces a single sorted iterator object containing the combined elements of the iterables.
import heapq
L1 = [23, 25, 27, 29, 31]
L2 = [0, 1, 2, 3, 4, 6]
L3 = [100, 150, 200, 250, 300]
print(list(heapq.merge(L1, L3, L2)))